Calculating Heat Flux
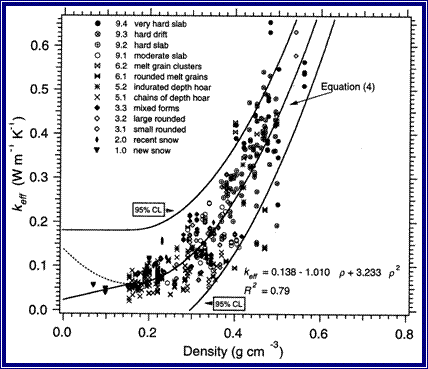
Figure 5.23: The relationship between snow density and snow thermal conductivity.
Image from Sturm, M., Holmgren, J., König, M, Morris, K. (1997.) Thermal conductivity of seasonal snow. Journal of Glaciology, 43 (143), 26-41.
Students in grades 3-12 can collect the data on snow and temperature needed for these calculations. Middle school and high school students can carry out the calculations needed to determine the conductive heat flow.
Conductive heat flow (Fa) (also known as heat flux) is a function of:
(a) snow temperature gradient (Ts–Tb/Zs); and
(b) snow thermal conductivity (keff).
Ts: snow surface temperature
Tb: snow bottom temperature
Zs: snow depth
keff: snow thermal conductivity
Snow thermal conductivity is a function of snow density.
As the density of snow increases, the rate at which heat can move through the snow (snow thermal conductivity) also increases. The PowerPoint on Conductive Heat Flow provides instructions for calculating heat flux. It also includes several “Thought Experiments”, designed to give you practice in thinking about the relationships between snow depth, snow density, and temperatures. See if you can answer the thought experiments. Try calculating heat flux using the examples in the PowerPoint.
While many scientists focus their research on heat flux using bodies of water, heat is also stored in the ground. It is interesting to compare data collected on snow-covered ground with data from the surface of an ice and snow-covered lake or pond. You can also compare data from different types of ground surfaces (sidewalks, grass, forested area, bare ground under a building, areas with compacted snow, etc.). Snow density and ground temperatures tend to vary significantly between different surfaces. The snow must have remained on the ground for a period of time, and the air temperature must remain fairly cold for a period of time, for the data to be meaningful.
In relatively deep snow, the longer the surface remains covered with snow, and the colder the air temperatures are, the more dramatic will be the differences between the surface of the snow and the base of the snow.