Polarity of Water

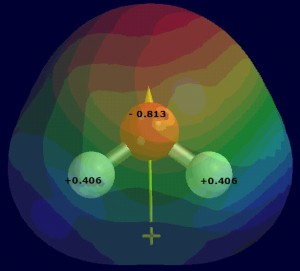
Figure 4.5: The partial charges and dipole moment for the water molecule. These partial charges result in water molecules being strongly attracted to one another in the solid and liquid phases.

The partial charges and dipole for the water molecule are shown in Figure 4.5; note that the charges are significantly larger than in carbon monoxide. These partial charges result in water molecules being strongly attracted to one another in the solid and liquid phases.

In other words, for a group of water molecules, the positively charged H-atoms are electrically attracted to the negatively charged O-atoms. You can think of this attraction as water molecules tending to stick together, and the results are interesting.

Check Your Thinking: Can you think of any physical properties of water that may result from molecular “stickiness”?

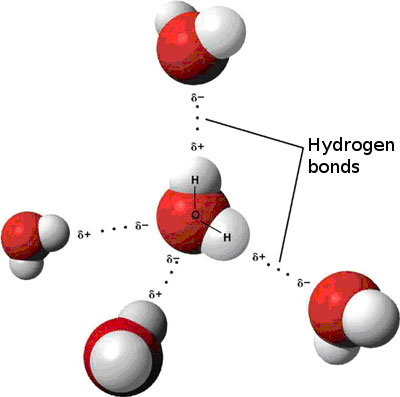
This strong electrostatic attraction between hydrogen atoms on one water molecule to oxygen atom on another is called Hydrogen Bonding, or H-bonds. Hydrogen bonds are labeled in Figure 4.6 below (the negative [-] oxygen atoms bond to the positive [+] hydrogen atoms). Each water molecule can make or accept two H-bonds.

Figure 4.6: Each water molecule can make or accept two H-Bonds, the strong attraction between hydrogen atoms on one water molecule to the oxygen atom on another water molecule.
Image from URL: http://en.wikipedia.org/wiki/Water